Using the Right Datastructure for the job
15 May 2015Searching for a key
The process of choosing the right data structure is one that few will ever think about, one that most take for granted. In my experience, this lack of curiosity, and more importantly, an aversion to experimenting and benchmarking can lead to unnecessary overhead. Let’s take an example. One of the most common operations of any software I’ve seen written is finding a key and acting upon that, whether that means checking whether it exists, doesn’t exist, or getting the associated value. We will narrow this down to finding whether the key exists or not for simplicity’s sake.
Additionally for the same purpose, let’s limit the key type to int. int this is probably the most common and well understood datatype in the language, and very likely used as an ‘id’ type in many different applications.
Alright, so we have an application that has integer id’s, perhaps for some customer identification system and we’re building a cache for it. Hitting or missing the cache answers the simple question “Should we query the database?” Now, the obvious datastructure that pretty much every computer science major would choose here is the hashmap, which in C++ is now called the unordered_map. Why? Because Big O notation tells us the runtime of querying a hashmap is constant. What other options do we have?
- A vector, which under the hood is an array , aka contiguous memory.
- A tree, which can give us sorted traversal, but has a lot of pointers and possibly page faults
- A Linked list
There’s more but I’m going to stop there. Why would we choose anything else when Big O tells us a hashmap is good enough? Sometimes Big O behavior is not indicative of our application. Sometimes we want small O. What do I want you to take away from this? Measure Everything. Get into the habit of measuring tasks, as it’s the only way you can get “true” answers, in terms of prediction performance on your machine. Some people might say, “Use a vector! We can optimize cache lines that way!” Well, the truth is, I don’t know which is the best one, but say hack something together.
Key generation
#include <random>
#include <chrono>
std::random_device rd;
std::mt19937 gen(rd());
std::uniform_int_distribution<> dis( 0, MAX_VAL );This is our key supplier, giving us a predictable range of keys in a uniform distribution. We can use dis as much as we want, and be confident that as the number of keys grows, the keys will fall in line with a uniform distribution.
### Building the Index
// initialize datastructures
std::unordered_map<int,int> myMap;
std::vector<int> myVector;
// generate keys
std::cout << "Generating keys." << std::endl;
for (size_t i = 0; i != NUM_KEYS; ++i) {
int key = dis(gen);
int val = dis(gen);
if (myMap.find(key) == myMap.end()) {
myMap[key] = val; // add key,value to map
myVector.push_back(key);
}
}
Here we populate the same keys to both the map and the vector and any other data structures we’d like to measure. This gives us comparable performance, as well as a method to check the correctness of our code, aka. did the same queries give us the same results for both data structures?
Building Queries
std::cout << "Generating Queries." << std::endl;
std::vector<int> queries;
queries.resize(NUM_QUERIES);
for (size_t i = 0; i != NUM_QUERIES; ++i) {
queries[i] = dis(gen);
} This is important. We are generating the queries beforehand and storing them. This accomplishes several things:
- the cost of generating a query is not baked into the measurement of querying
- The same queries can be executed on both the map and the vector
- If we wanted, the queries could be manipulated in several ways [ sorted, shuffled, etc.]
Querying
// query map and time duration
std::cout << "Querying map..." << std::endl;
std::chrono::time_point<std::chrono::system_clock> start, end;
start = std::chrono::system_clock::now();
int numMatchesMap = 0;
for (size_t i = 0; i != NUM_QUERIES; ++i) {
if (myMap.find(queries[i]) != myMap.end())
++numMatchesMap;
}
end = std::chrono::system_clock::now();
std::chrono::duration<double> elapsed_seconds = end-start;
std::cout << "Elapsed time for " << NUM_QUERIES << " queries in map:"
<< elapsed_seconds.count()
<< "\nNum matches in map: " << numMatchesMap
<< "\nQuerying vector..."
<< std::endl;
The task here is simple, serially iterate through the queries, and check whether they exist or not in the index. Time the duration it takes to run through all the queries and do this check. Afterwards, output the results. The code is quite similar for the vector so I won’t include that here, but I’ll post the source.
Results
Alas, our computer science professors taught us well. A hashmap is the way to go. Or is it? I had several parameters, one of which we varied. I kept the keyspace limited to 10000 for the purpose of clarity.
// constants
int NUM_KEYS = atoi(argv[1]);
int MAX_VAL = atoi(argv[2]);
int NUM_QUERIES = 1000000;| Number of Keys | Unordered Map Query Time (s) | Vector Query Time (s) |
|---|---|---|
| 5 | 0.092408 | 0.048035 |
| 10 | 0.095659 | 0.067716 |
| 20 | 0.100039 | 0.130688 |
| 50 | 0.087938 | 0.254695 |
| 100 | 0.081867 | 0.479975 |
| 200 | 0.098481 | 0.888507 |
| 400 | 0.096329 | 1.73241 |
| 800 | 0.098282 | 3.29157 |
| 1600 | 0.097052 | 6.12024 |
| 3200 | 0.093558 | 10.463 |
| 6400 | 0.093106 | 16.1336 |
For almost every experiment, the unordered map beats out the vecto, sometimes by several orders of magnitude. The vector does win out when you have a very small number of keys ( < 10 ). Imagine a scenario where you have an application that is distributing queries to a cluster of machines, where the number of machines is quite low and the number of queries is very high. A vector might be the right choice here over the unordered map. But for almost everything else, use a hashmap.
Compound Keys
There will come a time in every software engineer’s life where he’ll want to combine two keys to make a single key. An application might need to know given a domain id, does a user id exist. In a library application, we might need to key off the author and book title. Whether there are values involved or not is not as important. This circumstance has happened to me several times, and by default, I chose the option that came easiest to me to think of. More often than not, this isn’t the best option. Better would be to measure and understand the tradeoffs between several options.
Datastructures
The solution I defaulted to was creating a compound key, and creating some makeshift hasher for that. This compound key and hasher would be used to create the unordered_map.
. This is another potential solution by splitting up the two keys by making one the key of the unordered map, and the second part of value of the first key, in the form of a vector of pairs(key 2, value).
There are other solutions: trees, stacks, linear probing maps, etc. But for the purpose of demonstrating the process rather than the answer, I kept it to just these two. In the following sections, I’ll show code snippets of the hashing, key generation, query generation, and querying all in one go, since the idea is quite the same. The one thing I’ll explain is how to build a map with a compound key, aka creating a hash function. Everything below is self contained and can be compiled and run.
The Code
#include <unordered_map>
#include <algorithm>
#include <vector>
#include <list>
#include <random>
#include <chrono>
#include <ctime>
#include <iostream>
#include <string>
#include <assert.h>
template <class T>
inline void hash_combine(std::size_t & seed, const T & v)
{
std::hash<T> hasher;
seed ^= hasher(v) + 0x9e3779b9 + (seed << 6) + (seed >> 2);
}
namespace std
{
template<typename S, typename T> struct hash<pair<S, T> >
{
inline size_t operator()(const pair<S, T> & v) const
{
size_t seed = 0;
::hash_combine(seed, v.first);
::hash_combine(seed, v.second);
return seed;
}
};
}
int main(int argc, char** argv)
{
assert(argc == 3);
// constants
int NUM_KEYS = atoi(argv[1]);
int NUM_2ND_KEYS = atoi(argv[2]);
int MAX_VAL = 100000;
int NUM_QUERIES = 1000000;
// initialize random engine
std::random_device rd;
std::mt19937 gen(rd());
std::uniform_int_distribution<> dis( 0, MAX_VAL );
// initialize datastructures
std::unordered_map< std::pair<int,int>, int> myMap;
std::unordered_map< int, std::vector<int> > myMapVector;
typedef std::vector<int> IntVec;
// generate keys
std::cout << "Generating keys." << std::endl;
for (size_t i = 0; i != NUM_KEYS; ++i) {
int key = dis(gen);
for (size_t j = 0; j != NUM_2ND_KEYS; ++j)
{
int key2 = dis(gen);
int val = dis(gen);
if (myMapVector.find(key) == myMapVector.end()) {
myMapVector[key] = IntVec();
}
std::pair<int,int> compoundKey = std::make_pair(key,key2);
if (myMap.find(compoundKey) == myMap.end()) {
myMap[compoundKey] = val; // add key,value to map
myMapVector[key].push_back(key2);
}
}
}
std::cout << "Generating Queries." << std::endl;
std::vector< std::pair<int,int> > queries;
queries.resize(NUM_QUERIES);
for (size_t i = 0; i != NUM_QUERIES; ++i) {
queries[i] = std::make_pair(dis(gen), dis(gen));
}
//query map and time duration
std::cout << "Querying map" << std::endl;
std::chrono::time_point<std::chrono::system_clock> start, end;
start = std::chrono::system_clock::now();
int numMatchesMap = 0;
for (size_t i = 0; i != NUM_QUERIES; ++i) {
if (myMap.find(queries[i]) != myMap.end())
++numMatchesMap;
}
end = std::chrono::system_clock::now();
std::chrono::duration<double> elapsed_seconds = end-start;
std::cout << "Elapsed time for " << NUM_QUERIES << " queries in map:"
<< elapsed_seconds.count()
<< "\nNum matches in map: " << numMatchesMap
<< "\n Querying map vector"
<< std::endl;
// querying map vector
start = std::chrono::system_clock::now();
int numMatchesVector = 0;
for (size_t i = 0; i != NUM_QUERIES; ++i) {
if ( myMapVector.find(queries[i].first) != myMapVector.end() &&
std::find(myMapVector[queries[i].first].begin(),
myMapVector[queries[i].first].end(),
queries[i].second) !=
myMapVector[queries[i].first].end())
++numMatchesVector;
}
end = std::chrono::system_clock::now();
elapsed_seconds = end-start;
std::cout << "Elapsed time for " << NUM_QUERIES << " queries in map vector:"
<< elapsed_seconds.count()
<< "\nNum matches: " << numMatchesVector
<< std::endl;
}The hashing function was stolen from Boost, which provides, a decent way generalized way (templated) to combine hash functions of as many keys as you want. Here, since we’re only hasing a compound key, we called ::hash_combine on the first and second part of the pair, and specialized the template on that, so we can build unordered_maps with pairs as keys for any type that has been specialied for std::hash. Below is the repeat of the hashing functionality.
template <class T>
inline void hash_combine(std::size_t & seed, const T & v)
{
std::hash<T> hasher;
seed ^= hasher(v) + 0x9e3779b9 + (seed << 6) + (seed >> 2);
}
namespace std
{
template<typename S, typename T> struct hash<pair<S, T> >
{
inline size_t operator()(const pair<S, T> & v) const
{
size_t seed = 0;
::hash_combine(seed, v.first);
::hash_combine(seed, v.second);
return seed;
}
};
}Results
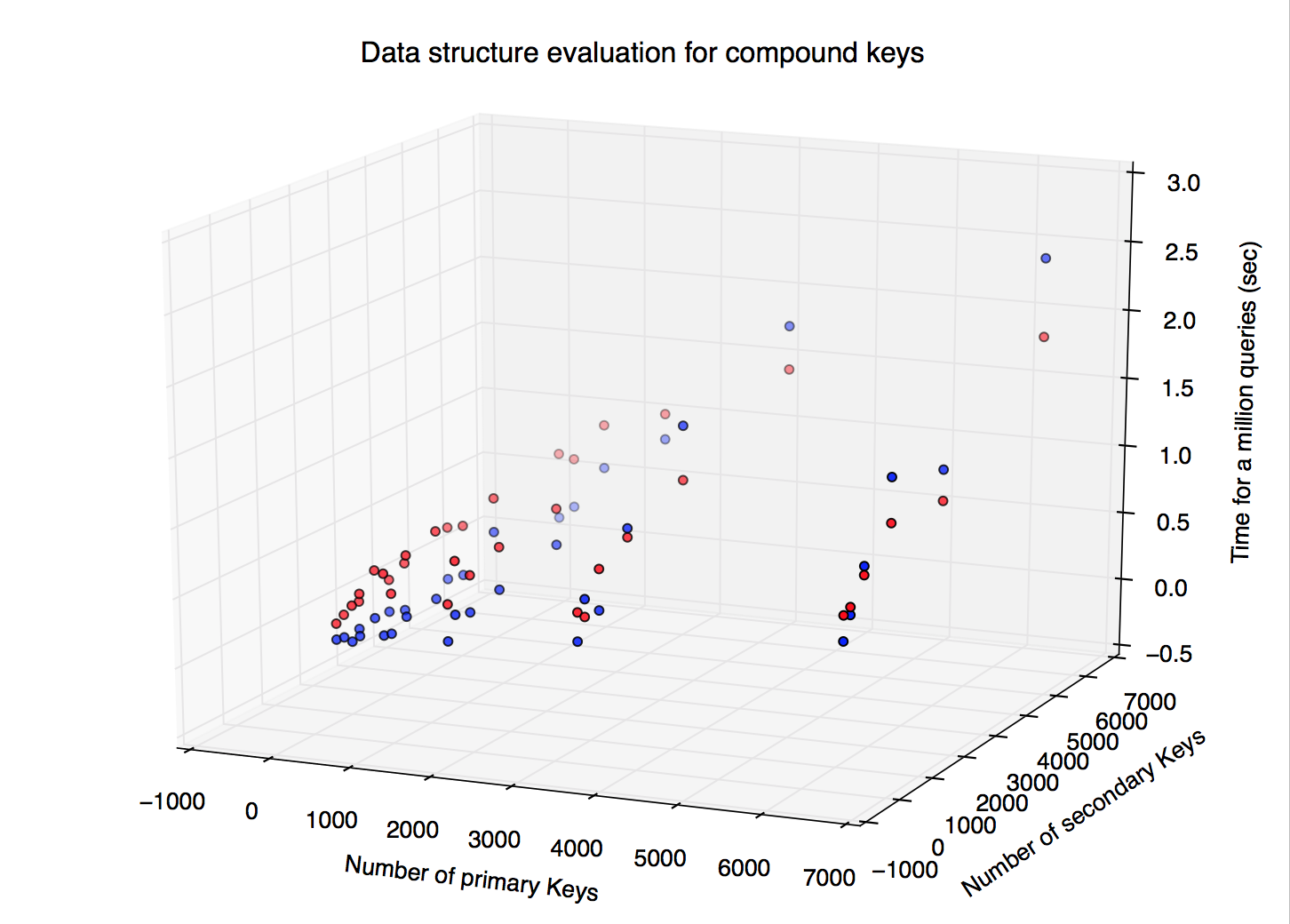
The 3d scatter plot shows two dependent variables for the x and y axes, and the ouput variable on the z axis.
- X: the number of primary keys in data structure
- Y: the number of secondary keys for each primary key
- Z: the real time to query each data structure for 1 Million Queries
The red points in the scatter plot are the measurements for std::unordered_map<compound key, value>, where as the blue points represent the timings for the unordered_map<key 1, vector<key 2, value> >. For the majority of cases, the unordered_map<key 1, vector<key 2, value> > beats out the std::unordered_map<compound key, value>, defying Big O analysis which would predict constant time querying for the compound key map.
Analysis
Having a mediocre hash function can crush performance
Using a compound key forces us to come up with an ad-hoc hash function. While the hash functions for primitive types such as integers tend to be uniform and well studied, those of combined forms are most likely not. We stole Boost’s ::hash_combine implementation, yet our performance still degraded. Bad hashing functions lead to collisions and adding additional links in our linked list see how a hashmap works here. Navigating linked lists lead to a lot of pointer look ups, aka more cache misses.
On the flipside, the unordered_map<key 1, vector<key 2, value> > has predictable look up performance, since the hashing is only applied on a single integer instead of combining two of them. Once we find the vector, scanning through the vector is fast because of locality of reference.
Main takeaway
The point of this exercise is not to tell you which data structure to use, but to hopefully lead you to answer these questions on your own, depending on the application. The bread of this experiment had many assumptions baked in like limiting the key space to an arbitrary value or randomizing the queries. These are not necessarily indicative of your own application - it is up to you to decide which parameters to vary and how to build an experiment as close to reality as possible. Perhaps, your key space is limited to under 1000. Or maybe there will be many secondary key look ups for the same primary key sequentially.
This sort of exercise is useful for every engineer, and vital to build low-latency applications. Hope this helps! Happy benchmarking.